What's this?…
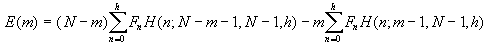
What's this?… | 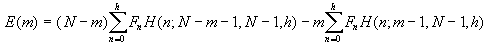 |
Monte Carlo simulations are probabilistic (hence the name, according to legend; Monte Carlo, gambling, roulette wheel, probabilities,...) -- they explore complex behaviour based on carefully chosen probabilty functions. Suppose we wanted to use Monte Carlo techniques to simulate the way lines form behind R cash registers. We could come up with a probability function A(t) which gives the probability that a customer arrives at time t and another function that give the probability that the customer chooses a particular register's line: L(r), where r is the register number, 1, 2,..R. We could spend a happy hour, day or month coding this up and then let it run. The trick here would be in formulating L so that it embodies, as accurately as possible, the way people really choose a line. Clearly, it's a function of the line length, but there is probably also a contribution from a rule along the lines of "the customer is less likely to go to the same line the previous customer chose". You'd also need a probability function that gave the time required for a front customer to finish at the register and leave the line. If you added a function that gave the time the arriving customer took to decide which line to join (oh dear, a line may form to choose a line) you could mix in some logic based on the new customer's perception of how rapidly a line is travelling (unless these people know they're mere simulations and that it's entirely random). OK, this is no longer a simple example.
The Ising Model simplifies ferromagnetic materials by supposing that they consist of tiny magnetic monopoles spinning either up or down. These upspins and downspins are coupled to their immediate neighbours.
My project entailed coding a Monte Carlo simulation of the Ising model. I had an 2D array of cells and would repeatedly sweep through it, updating each cell's state, according to the model's rules. What I was looking for was the characteristic phase change. This was done using some variant of BASIC on the University's PRIME mainframe. It was slow, but I did get that transition. One day I was sitting in the James Haight library building, writing up the project. I remember it was on the first floor, that long line of tables that face out toward the Computer Science department (to the left) and the University Bookshop (to the right). My eyes were probably very dry from those damn hot-air vents (I'm assuming some people reading this will know what I'm talking about). Anyway, I was cogitating, as one does, and thought something along the lines of
I'm explicitly passing through the array and looking at the number of upspin neighbours around each cell in turn. The distribution of upspins in the array is random. Shouldn't I be able to compute the probability that I'll find n upspins, given the total number? If I can do that, I can compute the expected number of transitions and write an equation that will just iterate the total number of upspins.It was one of those rare "Aha!" moments. They don't always pan out, but this one did. I had to spend some time doing research into Probability theory (a subject I've always found "difficult", like Chemistry) to find the Hypergeometric probability function. This distribution,
H(n;D,P,S), represents the probability that, if a sample of
size S is taken without replacement from a "population" of size P which contains
D "defectives", then n of the sample will be defective:
H(n;D,P,S) = DCn(P-D)C(S-n)/PCSwhere
xCy = x!/y!(x-y)!(the binomial coefficient). I won't bore you with the details, but from this I was able to come up with the Emulator. This let me do "virtual" Monte Carlo runs -- I didn't need to pass through a real array, I could just simulate what would happen "on average" by iterating:
upspinsi+1 = upspinsi + E(upspinsi)It actually worked -- I saw a phase change in the Emulator data and I included my results in the project report. As far as I know this idea was new. I consider myself very lucky to've actually come up with something original in Physics (well, I guess it's mostly Mathematics). I'd be interested in hearing from anyone who's seen the Emulator (or a variant) before.